
Zadanie Podciągi arytmetyczne (art)
Pomóż nam usprawnić bazę zadań!
Podciągi arytmetyczne
Limit pamięci: 32 MB
Masz podaną pewną permutację liczb 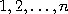 dla pewnego
dla pewnego  .
Niech kolejne liczby permutacji tworzą ciąg
.
Niech kolejne liczby permutacji tworzą ciąg 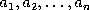 .
Twoim zadaniem jest policzenie, ile istnieje arytmetycznych podciągów
ciągu
.
Twoim zadaniem jest policzenie, ile istnieje arytmetycznych podciągów
ciągu  o długości równej 3. Dokładniej, musisz zliczyć trójki
o długości równej 3. Dokładniej, musisz zliczyć trójki 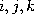 takie
że
takie
że 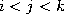 oraz
oraz 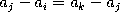 .
.
Wejście
W pierwszej linii wejścia znajduje się jedna liczba całkowita 
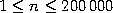 . Drugi wiersz zawiera
. Drugi wiersz zawiera  liczb
całkowitych
liczb
całkowitych 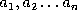 , reprezentujących naszą permutację.
, reprezentujących naszą permutację.
Możesz założyć, że w testach wartych przynajmniej 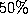 punktów zachodzi
dodatkowy warunek
punktów zachodzi
dodatkowy warunek 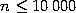 .
.
Wyjście
Na wyjściu należy wypisać liczbę podciągów arytmetycznych o długości 3 dla permutacji z wejścia.
Możesz założyć, że wynik nie przekroczy 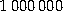 .
.
Przykład
Dla danych wejściowych:
5 1 5 4 2 3
poprawną odpowiedzią jest:
2
Autor zadania: Adrian Jaskółka.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English